Oberoende händelser och träddiagram
Snabbguide
- Oberoende händelser påverkar inte varandras sannolikheter. Sannolikheten för en händelse är densamma oavsett vad som händer med den andra händelsen.
- Sannolikheten för två oberoende händelser, A och B, beräknas som \( P(A \text{ och } B) = P(A) \cdot P(B) \).
- Träddiagram för oberoende händelser visar alla möjliga utfall för varje händelse, och sannolikheterna för varje gren är desamma oavsett tidigare utfall.
- För att läsa ett träddiagram, följ grenarna och multiplicera sannolikheterna längs vägen för att hitta den totala sannolikheten för ett utfall.
Oberoende händelser är händelser där utfallet av en händelse inte påverkar sannolikheten för den andra händelsen. I denna genomgång kommer vi att utforska hur man identifierar oberoende händelser och hur man använder träddiagram för att illustrera och beräkna sannolikheten för sådana händelser.
Vad är oberoende händelser?
Två händelser, A och B, sägs vara oberoende om sannolikheten för att B inträffar inte påverkas av om A inträffar eller inte. Det innebär att sannolikheten för B är densamma, oavsett vad som händer med A.
Exempel: Om du kastar en tärning och singlar en slant, är dessa två händelser oberoende av varandra. Resultatet av tärningskastet påverkar inte resultatet av slantsinglingen, och vice versa.
Beräkning av sannolikhet för oberoende händelser
Sannolikheten för att två oberoende händelser, A och B, båda inträffar kan beräknas med formeln:
\[ P(A \text{ och } B) = P(A) \cdot P(B) \]
Här är:
- \( P(A) \): Sannolikheten att A inträffar.
- \( P(B) \): Sannolikheten att B inträffar.
Exempel: Kasta en tärning och singla en slant
Vad är sannolikheten att få en 4 på en tärning och klave på en slant?
- Tärningskast: Sannolikheten att få en 4 är \( \frac{1}{6} \).
- Slantsingling: Sannolikheten att få klave är \( \frac{1}{2} \).
\[ P(\text{4 och Klave}) = \frac{1}{6} \cdot \frac{1}{2} = \frac{1}{12} \approx 0.0833 \]
Sannolikheten att få både en 4 på tärningen och klave på slanten är cirka 8,33%.
Träddiagram för oberoende händelser
Ett träddiagram är ett visuellt hjälpmedel som kan användas för att visa alla möjliga utfall av en serie oberoende händelser. Eftersom varje händelse är oberoende av de andra, är sannolikheten för varje gren densamma oavsett vad som hänt tidigare. Låt oss titta på ett exempel med att kasta en tärning och singla en slant.
Exempel: Träddiagram för tärningskast och slantsingling
Vi använder samma exempel som tidigare: Vad är sannolikheten att få en 4 på en tärning och klave på en slant?
Träddiagrammet ser ut så här:
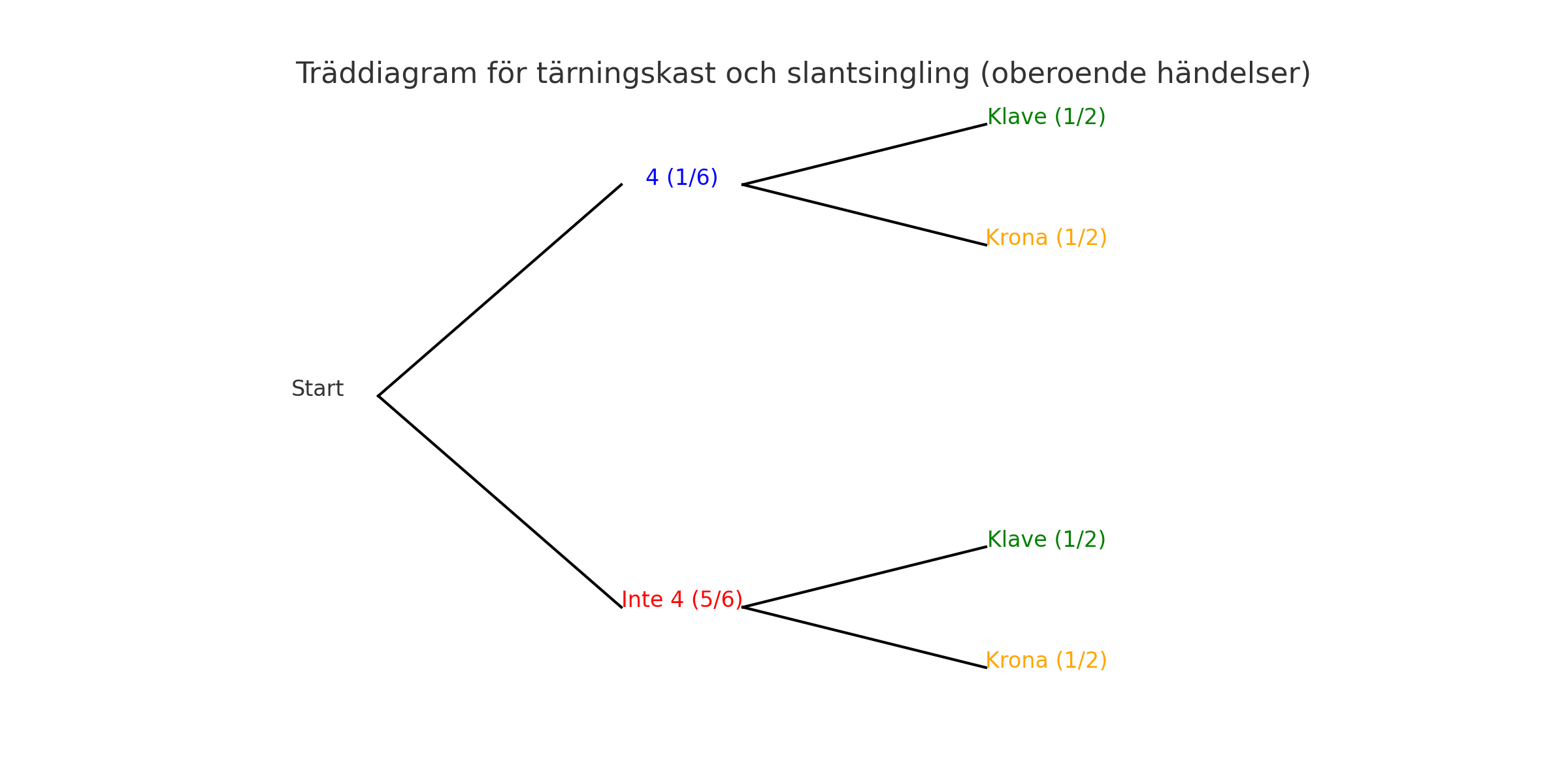
I träddiagrammet ser vi alla möjliga utfall för tärningskastet och slantsinglingen, och varje gren visar sannolikheten för just det utfallet.
Hur man läser av ett träddiagram
För att läsa av ett träddiagram för oberoende händelser följer du grenarna från vänster till höger. För varje steg multiplicerar du sannolikheterna längs grenarna för att få den totala sannolikheten för just det utfallet. Till exempel, om vi vill hitta sannolikheten att få en 4 och klave, följer vi grenarna "4" → "Klave" och multiplicerar sannolikheterna för dessa grenar.
Vanliga frågor
Sammanfattning
Oberoende händelser innebär att sannolikheten för en händelse inte påverkas av utfallet av en annan händelse. Träddiagram är ett användbart verktyg för att visualisera och beräkna sannolikheterna för oberoende händelser.