Avståndsformeln
Avståndsformeln används för att beräkna avståndet mellan två punkter i ett koordinatsystem. Om vi har två punkter med koordinaterna \( (x_1, y_1) \) och \( (x_2, y_2) \), kan avståndet mellan dessa punkter beräknas med hjälp av avståndsformeln:
Snabbguide
- Avståndsformeln: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Baseras på Pythagoras sats: Avståndet motsvarar hypotenusan i en rätvinklig triangel.
- Användningsområden: Beräkna avstånd mellan punkter, längden på linjer och radier i cirklar.
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Förklaring av formeln
Formeln bygger på Pythagoras sats. Om vi tänker oss en rätvinklig triangel där de två punkterna \( (x_1, y_1) \) och \( (x_2, y_2) \) utgör två av hörnen, kan vi se att avståndet mellan punkterna motsvarar hypotenusan i triangeln.
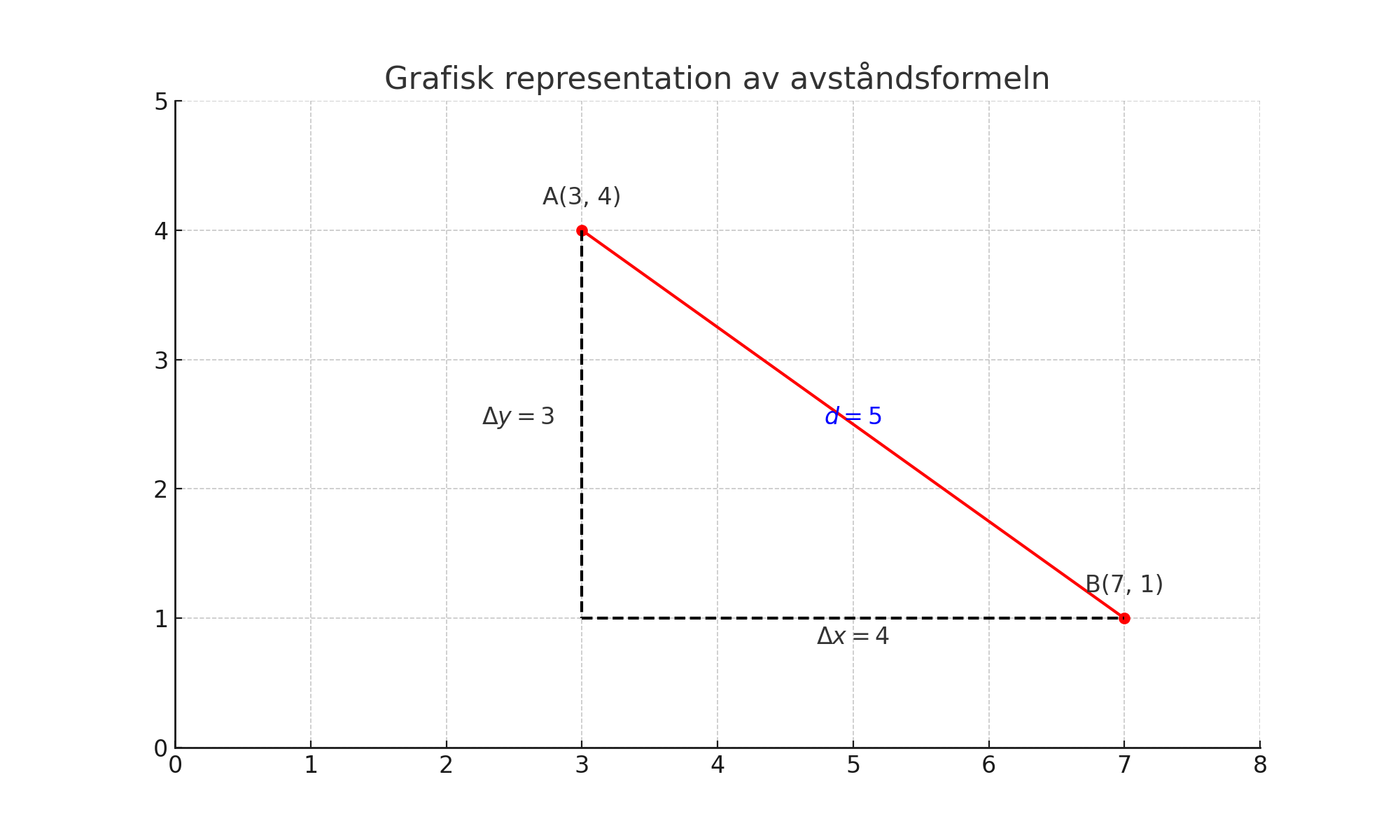
I figuren ovan representerar \( \Delta x \) skillnaden i x-koordinaterna och \( \Delta y \) skillnaden i y-koordinaterna mellan punkterna. Genom att använda Pythagoras sats får vi:
\[ d = \sqrt{(\Delta x)^2 + (\Delta y)^2} \]
Exempel: Beräkna avståndet mellan två punkter
Vad är avståndet mellan punkterna \( A(3, 4) \) och \( B(7, 1) \)?
För att beräkna avståndet använder vi avståndsformeln:
\[ d = \sqrt{(7 - 3)^2 + (1 - 4)^2} = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \]
Avståndet mellan punkterna \( A \) och \( B \) är 5 enheter.
Tillämpningar av avståndsformeln på högskoleprovet
Avståndsformeln har många tillämpningar inom geometri och trigonometri. Några exempel är:
- Beräkna avståndet mellan två punkter i ett koordinatsystem.
- Tidseffektivt i jämförelse med pythagoras sats vilket är kritiskt för dig som gör högskoleprovet.
- Bestämma längden på en linje som förbinder två punkter.
- Använda formeln för att beräkna radien i en cirkel när man känner till två punkter: cirkelns centrum och en punkt på cirkeln.
Vanliga frågor
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
Detta gör att du kan beräkna avståndet mellan två punkter i rymden.Sammanfattning
Avståndsformeln är ett användbart verktyg för att beräkna avståndet mellan två punkter i ett koordinatsystem. Genom att använda skillnaden mellan x- och y-koordinaterna, och tillämpa Pythagoras sats, kan vi snabbt hitta avståndet.