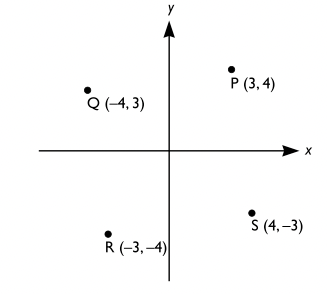
Vilken av punkterna $\boldsymbol{P, Q, R}$ och $\boldsymbol{S}$ ligger på linjen $\boldsymbol{3x + 4y = 0}$?
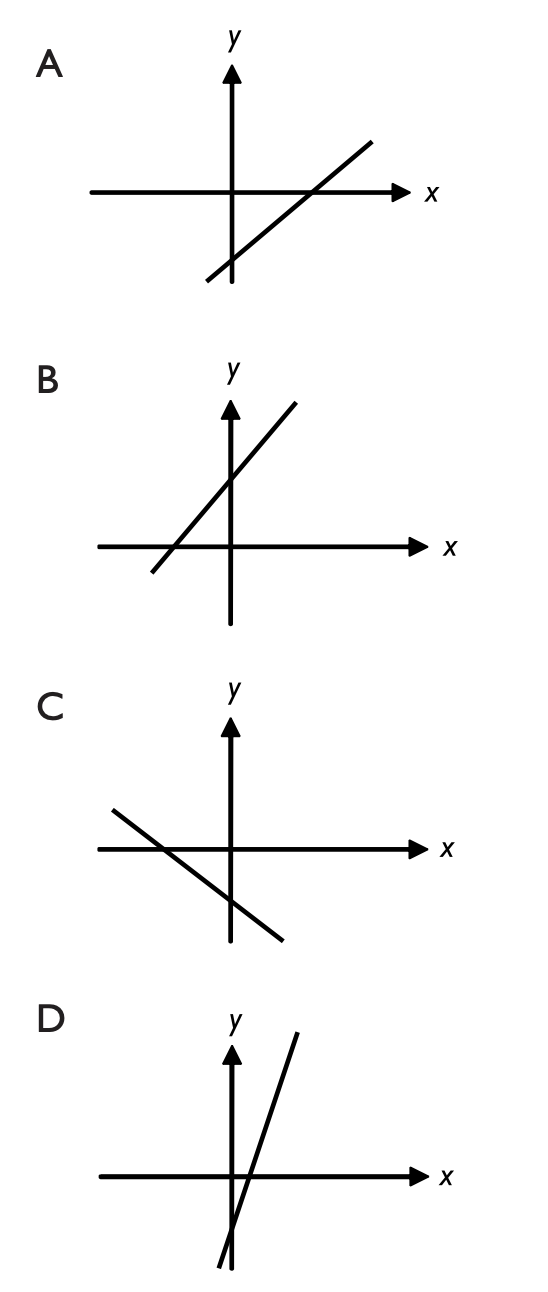
I svarsförslagen nedan är axlarna ritade i samma skala. Vilket svarsförslag motsvarar linjen $y = 3x – 3?$
$y = kx + m$ där konstanten $k \gt 0$ och konstanten $m \lt 0$. Hur förändras linjen om $\boldsymbol{m}$ multipliceras med $\boldsymbol{-1}$?
$f(x)$ är en linjär funktion vars graf går genom punkten $(0, 4)$ och skär grafen till $g(x) = -x - 2$ i en rät vinkel. Vad är $\boldsymbol{f(x)}$?
Vad är $\boldsymbol{y}$ då $\boldsymbol{x = -3}$?
Punkten $(3, 3)$ ligger på linjen $y = kx -3$.