Bestämma k och m grafiskt
Snabbguide
- Skärningspunkten med y-axeln, \( m \), är det y-värde där x är 0. Läs av detta värde direkt på grafen.
- För att hitta lutningen \( k \), välj en punkt på linjen, gå en enhet åt höger och se hur många steg du måste gå upp eller ned för att återkomma till linjen.
- Lutningen \( k \) är antalet steg upp eller ned per enhet åt höger.
- Ingen beräkning behövs, allt kan läsas av grafiskt!
Att bestämma k- och m-värdet i räta linjens ekvation, \( y = kx + m \), kan göras grafiskt utan att behöva göra några beräkningar. Vi kan enkelt läsa av grafen och förstå linjens egenskaper. I denna genomgång använder vi linjen \( y = 2x + 3 \) som exempel för att visa hur vi kan hitta både lutningen (k) och skärningspunkten (m) med hjälp av grafen.
1. Bestämma skärningspunkten med y-axeln (m)
Skärningspunkten med y-axeln är punkten där linjen korsar y-axeln, alltså där x är 0. För att hitta m-värdet i grafen behöver vi bara läsa av y-värdet vid x = 0.
Om vi tittar på linjen \( y = 2x + 3 \) ser vi att när x är 0, är y = 3. Detta innebär att linjen skär y-axeln vid punkten (0, 3). Därför är:
\[ m = 3 \]
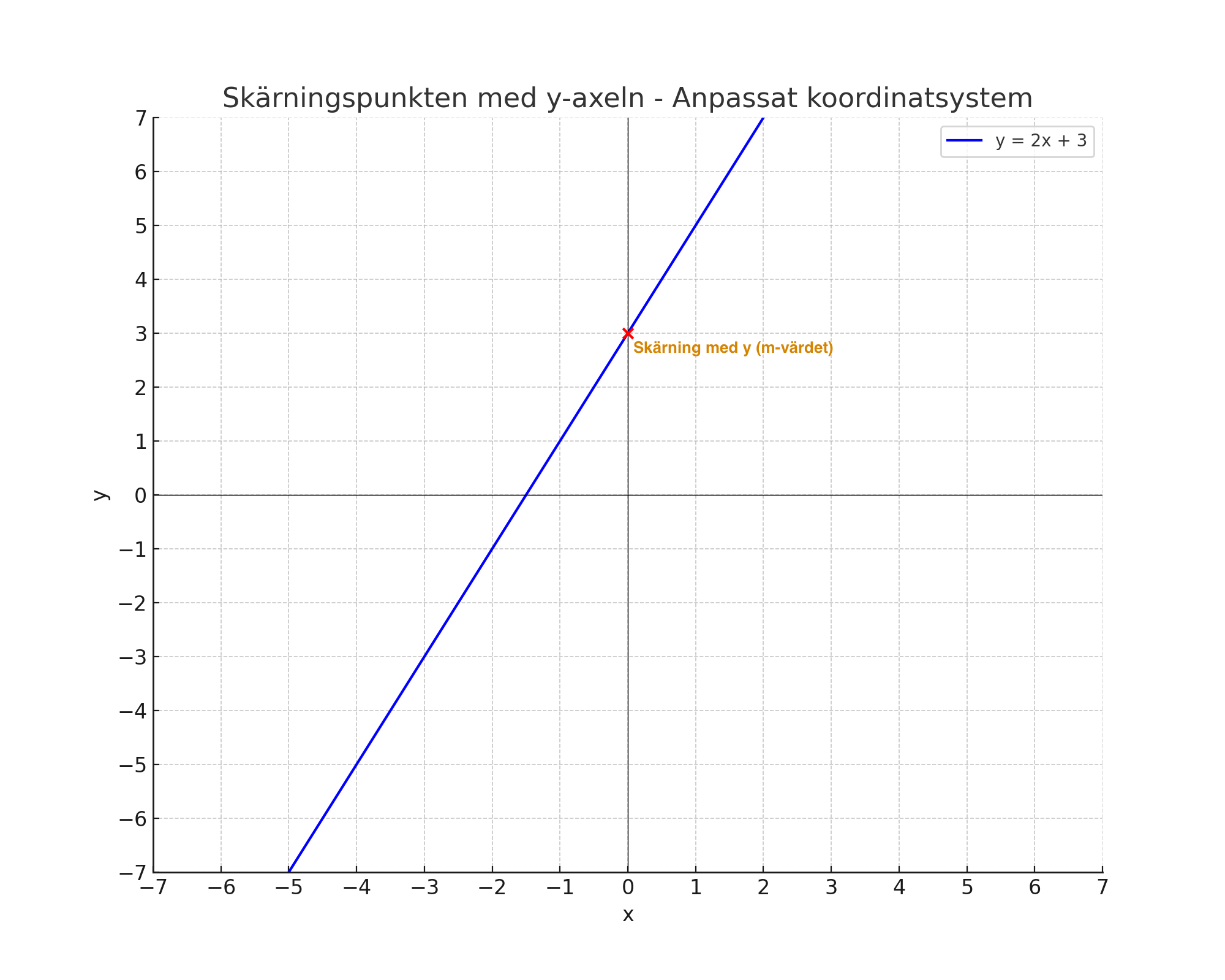
Detta är m-värdet, och vi kan se det direkt på grafen utan att behöva göra några beräkningar. M värdet är alltså värdet på \(y\) axeln vid den punkt \( x = 0 \)
2. Bestämma lutningen (k) grafiskt
Lutningen \( k \) bestämmer hur brant linjen är. För att hitta k-värdet grafiskt, kan vi använda följande steg:
Steg för att bestämma lutningen grafiskt:
- Ställ dig på en punkt på linjen: Välj en tydlig punkt där linjen passerar ett koordinatkryss, exempelvis (0, 3).
- Gå en enhet åt höger: Flytta en enhet åt höger i koordinatsystemet, alltså öka x-värdet med 1.
- Räkna antalet steg upp eller ned: Se hur många steg du måste gå upp eller ned för att komma tillbaka till linjen. Detta antal är lutningen k.
Exempel: Bestämma k för linjen \( y = 2x + 3 \)
Utgångspunkt: Välj punkten (0, 3).
- Gå en enhet åt höger: Vi flyttar från x = 0 till x = 1.
- Gå upp två steg: För att komma tillbaka till linjen går vi upp två enheter, från y = 3 till y = 5.
Detta innebär att lutningen \( k \) är 2. Varje gång vi går en enhet åt höger, går vi två enheter upp vilket demonstreras i bilden nedan.
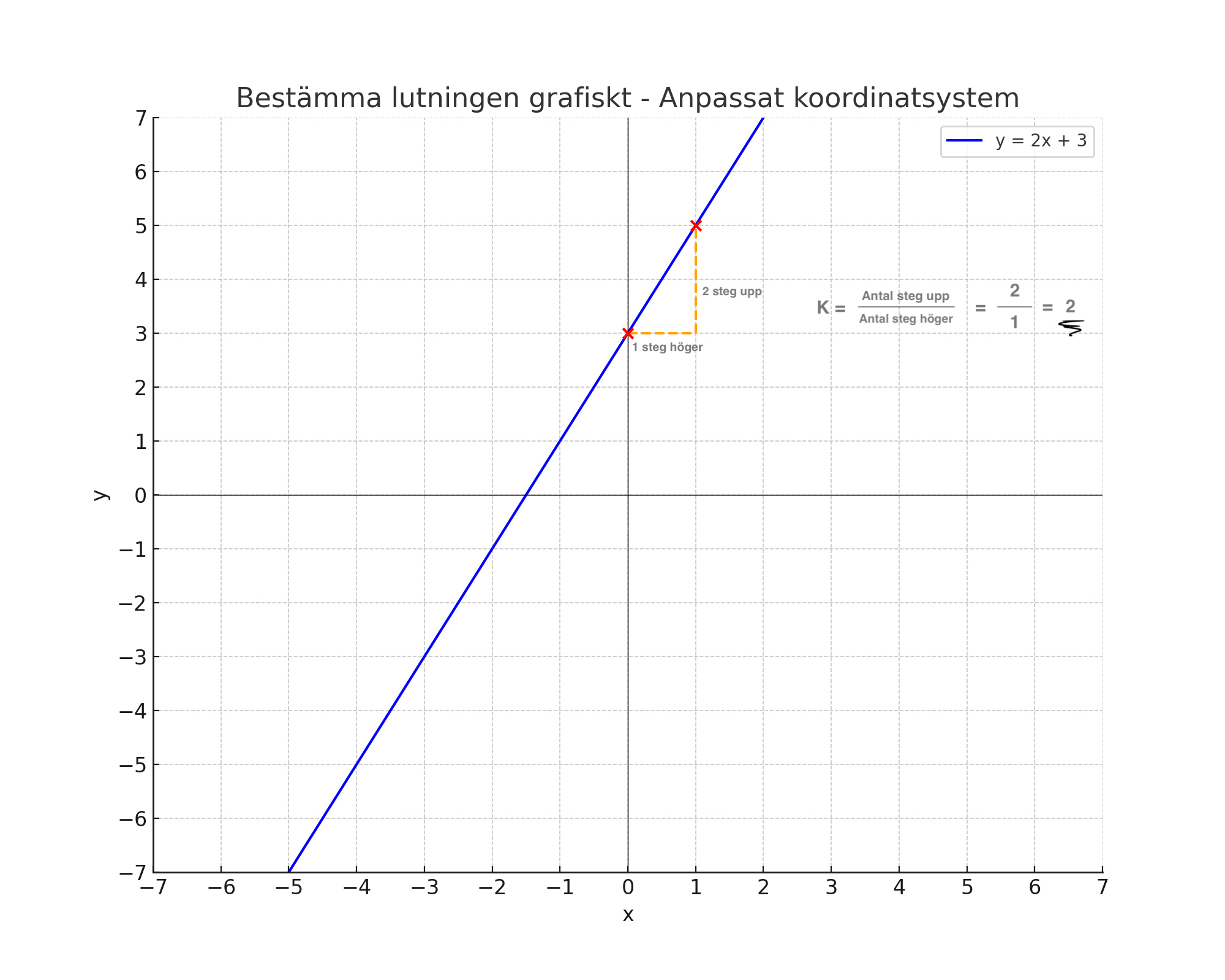
Grafisk representation av lutningen
Här visar vi hur lutningen kan ses grafiskt på linjen \( y = 2x + 3 \). Genom att välja två punkter och gå en enhet till höger samt två enheter upp, kan vi visuellt se att lutningen är 2.
Utgångspunkt: Punkterna (0, 3) och (1, 5).
- Från (0, 3) till (1, 5): Vi flyttar en enhet åt höger och två enheter upp. Detta visar att lutningen är 2.
Sammanfattning
Genom att använda grafen kan vi enkelt hitta både k- och m-värdet utan att behöva göra några beräkningar.