Introduktion till funktioner
Snabbguide
- En funktion kopplar varje inmatningsvärde till ett unikt utmatningsvärde.
- En funktion kan representeras som en formel, graf eller tabell.
- Definitionsmängden är alla möjliga inmatningsvärden, och värdemängden är alla möjliga utmatningsvärden.
- En linjär funktion har formen \( f(x) = ax + b \) och ger en rät linje som graf.
Funktioner är ett grundläggande koncept inom matematik och spelar en central roll i många områden, från algebra till kalkyl. En funktion beskriver ett samband mellan två mängder, där varje värde i den första mängden (inmatningsvärde eller x-värde) kopplas till ett specifikt värde i den andra mängden (utmatningsvärde eller y-värde). Att förstå funktioner är viktigt för att kunna analysera och lösa olika typer av matematiska problem.
Vad är en funktion?
En funktion är en regel som kopplar varje inmatningsvärde (kallas ofta x) till ett unikt utmatningsvärde (kallas ofta y). En funktion kan representeras på flera olika sätt, inklusive som en formel, en graf eller en tabell. Den generella formen av en funktion skrivs som:
\[ y = f(x) \]
Här är f funktionen, x är inmatningsvärdet, och y är utmatningsvärdet. Funktionen f bestämmer hur x och y är relaterade.
Exempel på en funktion
Exempel: En enkel funktion är:
\[ f(x) = 2x + 3 \]
Här tar funktionen in ett värde på x och multiplicerar det med 2, och adderar sedan 3. Om vi sätter in \( x = 4 \) i funktionen får vi:
\[ f(4) = 2 \times 4 + 3 = 8 + 3 = 11 \]
Så när x = 4 blir f(4) = 11.
Grafisk representation av funktioner
Funktioner kan också representeras grafiskt, där vi ritar varje punkt som motsvarar ett par av värden för x och y i ett koordinatsystem. I exemplet ovan skulle funktionen \( f(x) = 2x + 3 \) ge en rät linje i koordinatsystemet. Genom att analysera grafen kan vi snabbt se hur y-värdet förändras när x-värdet förändras.
Exempel på en graf
Exempel: Grafen för funktionen \( f(x) = 2x + 3 \) ser ut så här:
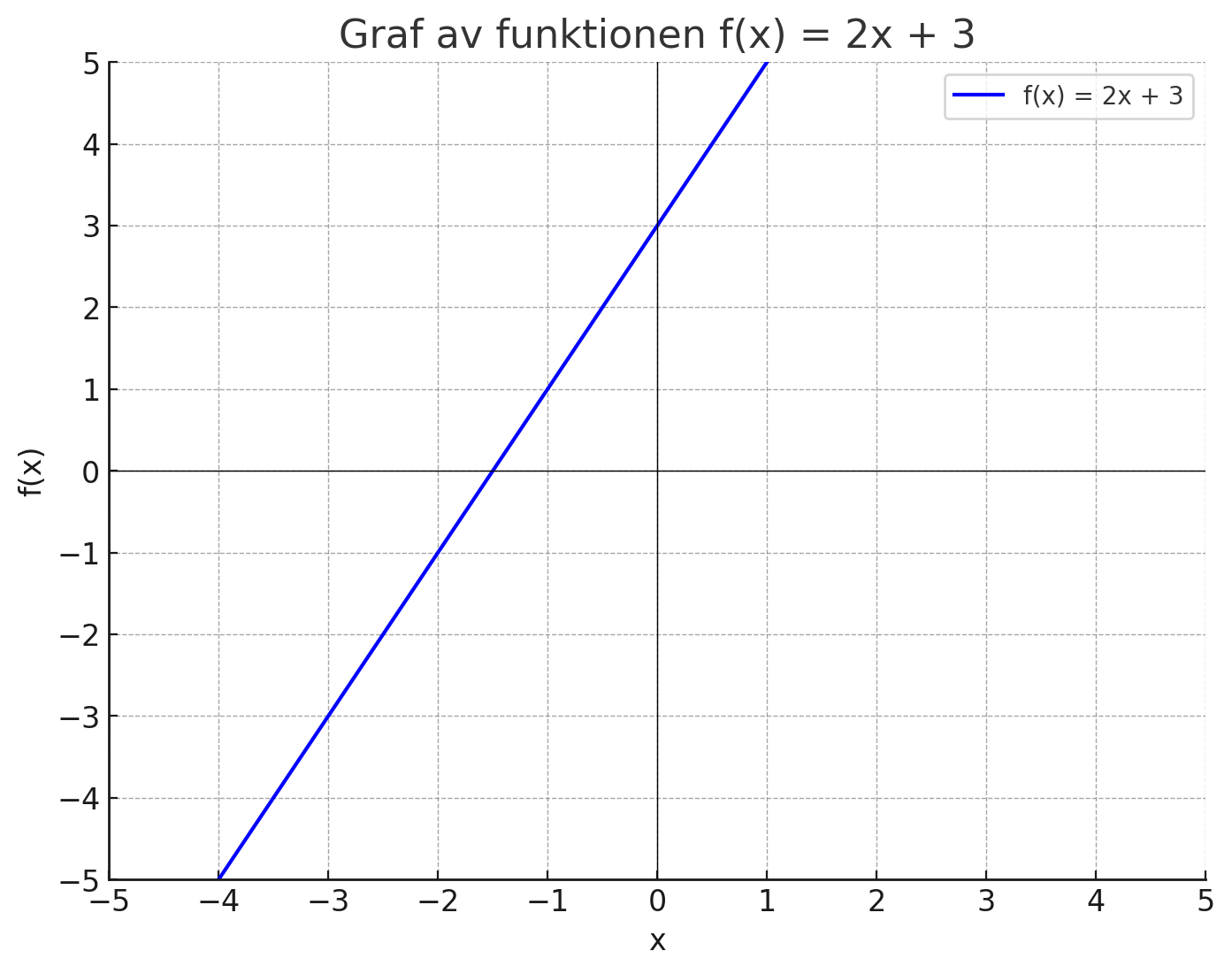
För att rita grafen, välj några olika värden på x, och beräkna y-värdet för varje x-värde.
- Om \( x = 0 \), då är \( f(0) = 2 \times 0 + 3 = 3 \).
- Om \( x = 1 \), då är \( f(1) = 2 \times 1 + 3 = 5 \).
- Om \( x = -1 \), då är \( f(-1) = 2 \times (-1) + 3 = 1 \).
Genom att plotta dessa punkter i ett koordinatsystem får vi grafen för funktionen.
Vanliga frågor
Sammanfattning
Funktioner är ett kraftfullt verktyg inom matematik som hjälper oss att beskriva och analysera förhållandet mellan olika variabler. Genom att förstå hur funktioner fungerar och hur de kan representeras på olika sätt, kan du lösa en mängd olika matematiska problem. Övning på att tolka funktioner grafiskt och algebraiskt kommer att göra dig mer bekväm med detta koncept.