Introduktion till räta linjens ekvation
Snabbguide
- Räta linjens ekvation: \( y = kx + m \).
- Lutningen \( k \) visar hur mycket y förändras när x ökar med 1.
- Skärningspunkten \( m \) är värdet på y när x är 0.
- En värdetabell hjälper oss att se sambandet mellan x- och y-värden.
- Från ekvationen kan vi rita en graf genom att välja x-värden och räkna ut motsvarande y-värden.
Räta linjens ekvation är en av de grundläggande byggstenarna inom algebra och beskriver en linjär funktion. Ekvationen \( y = kx + m \) beskriver ett samband mellan två variabler, där \( k \) är linjens lutning och \( m \) är skärningspunkten med y-axeln. Den här genomgången ger en introduktion till hur man arbetar med räta linjens ekvation, från värdetabell till ekvation och grafisk representation.
Vad är räta linjens ekvation?
Räta linjens ekvation beskriver en rak linje i ett koordinatsystem och har formen:
\[ y = kx + m \]
Här är:
- y: Det beroende värdet som vi får när vi sätter in ett x-värde i ekvationen.
- x: Det oberoende värdet som vi väljer.
- k: Lutningen på linjen, som beskriver hur mycket y-värdet förändras när x-värdet ökar med 1. Om \( k > 0 \) lutar linjen uppåt, och om \( k < 0 \) lutar linjen nedåt.
- m: Skärningspunkten med y-axeln, alltså det värde på y när x är 0.
Från värdetabell till ekvation
En värdetabell hjälper oss att förstå sambandet mellan x- och y-värden. Låt oss börja med ett exempel där vi har några x-värden och motsvarande y-värden.
Exempel: Värdetabell
Låt oss säga att vi har följande värden:
| x | y |
|---|---|
| -2 | -1 |
| 0 | 3 |
| 2 | 7 |
Vi kan observera att för varje ökning av x med 2, ökar y med 4. Detta indikerar att lutningen \( k = 2 \). Skärningspunkten med y-axeln är \( m = 3 \), eftersom när x är 0, är y 3.
Från värdetabell till ekvation
Nu när vi har lutningen och skärningspunkten kan vi skriva ekvationen för linjen:
\[ y = 2x + 3 \]
Denna ekvation beskriver sambandet mellan x och y för de givna värdena.
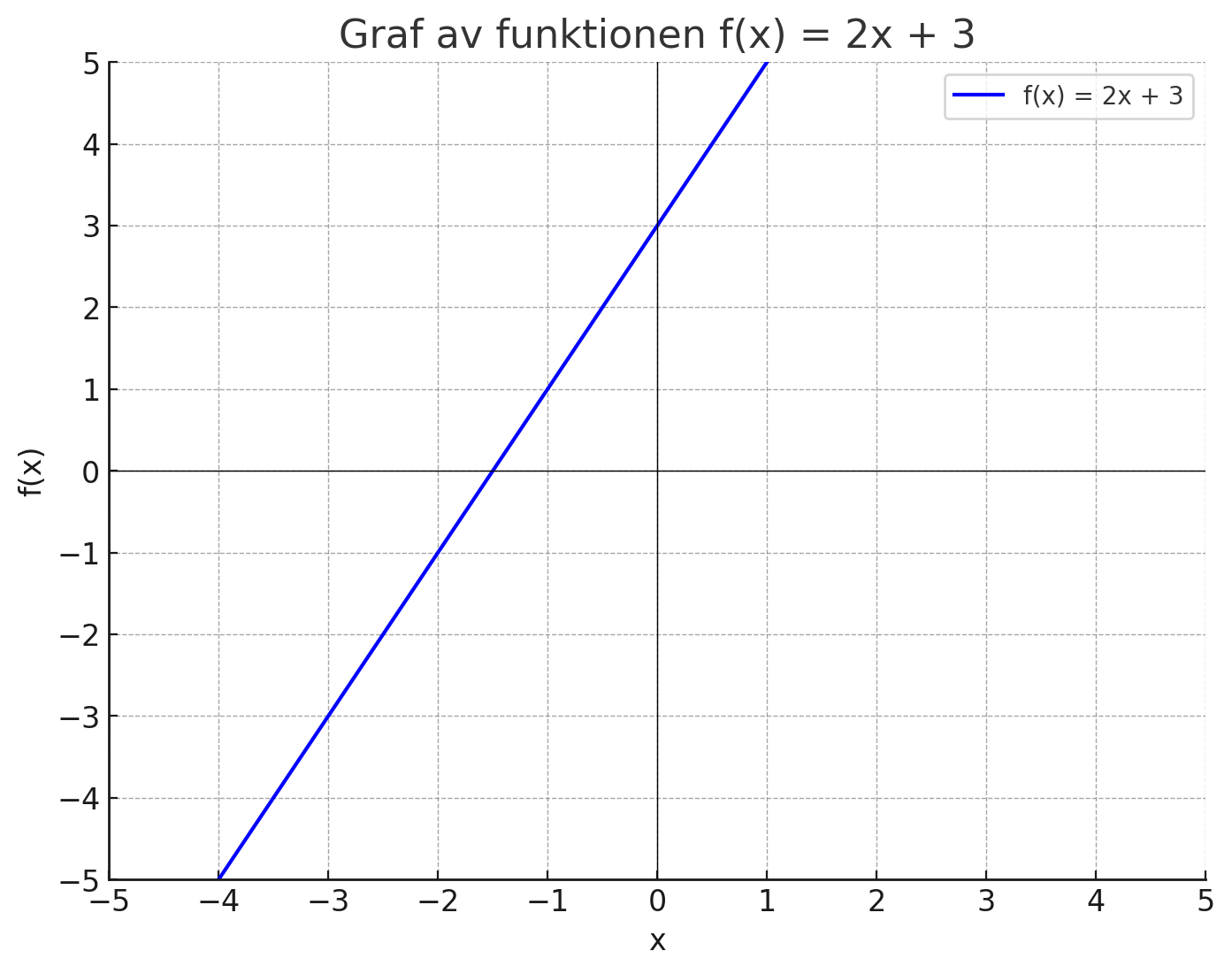
Från ekvation till graf
Nu när vi har ekvationen kan vi rita en graf för att visuellt se sambandet. Vi använder ekvationen \( y = 2x + 3 \) och plottar några punkter baserat på denna ekvation.
Exempel: Grafisk representation
Vi använder samma värden som i värdetabellen för att plotta punkterna på grafen:
- För \( x = -2 \) är \( y = 2 \times -2 + 3 = -1 \).
- För \( x = 0 \) är \( y = 3 \).
- För \( x = 2 \) är \( y = 2 \times 2 + 3 = 7 \).
Genom att rita en linje genom dessa punkter får vi grafen för linjen \( y = 2x + 3 \).
Vanliga frågor
Sammanfattning
Räta linjens ekvation är ett kraftfullt verktyg för att beskriva linjära samband. Genom att förstå hur vi kan gå från värdetabell till ekvation och graf kan vi lätt analysera och tolka linjära funktioner.