Funktioner grafiskt

Snabbguide

  • För varje x-värde finns ett unikt y-värde som kan läsas av på grafen.
  • Linjär funktion: En rät linje, formeln \( f(x) = ax + b \).
  • Kvadratisk funktion: En parabel, formeln \( f(x) = ax^2 + bx + c \).
  • Exponentialfunktion: Snabb tillväxt eller minskning, formeln \( f(x) = a^x \).
  • Nollställen: Där grafen skär x-axeln, \( f(x) = 0 \).
  • Extrempunkter: Maxima eller minima på grafen, där lutningen (derivatan) är 0.

Att förstå funktioner grafiskt är en viktig del av matematiken och hjälper oss att visualisera och analysera hur olika typer av funktioner beter sig. En graf av en funktion visar sambandet mellan inmatningsvärdet, som ofta kallas x, och utmatningsvärdet, som ofta kallas y. För varje x-värde kan vi hitta ett y-värde på grafen, vilket visar hur funktionen beter sig vid det specifika x-värdet.

Tolka en graf

När vi tolkar en graf letar vi efter följande egenskaper:

  • Nollställen: Punkterna där grafen skär x-axeln, alltså där \( f(x) = 0 \).
  • Skärningspunkt med y-axeln: Punkten där grafen skär y-axeln, vilket motsvarar värdet på funktionen när \( x = 0 \).
  • Värdet av funktionen: För varje x-värde kan vi läsa av grafen för att hitta motsvarande y-värde, vilket visar hur funktionen beter sig vid detta x-värde.

Att kunna läsa av och tolka grafer är viktigt för att förstå hur funktioner fungerar och för att kunna använda dem i problemlösning.

Linjär funktion

En linjär funktion är den enklaste typen av funktion och kan representeras med en rak linje. Den allmänna formen av en linjär funktion är:

\[ f(x) = ax + b \]

Här är \( a \) linjens lutning och \( b \) är skärningspunkten med y-axeln. Lutningen \( a \) visar hur mycket y-värdet förändras när x-värdet ökar med 1 enhet. Om lutningen är positiv lutar linjen uppåt, och om lutningen är negativ lutar linjen nedåt.

Exempel: \( f(x) = 2x + 3 \)

Denna funktion har en lutning på 2, vilket innebär att y-värdet ökar med 2 för varje enhet som x ökar. Skärningspunkten med y-axeln är 3. Grafen för funktionen ser ut så här:

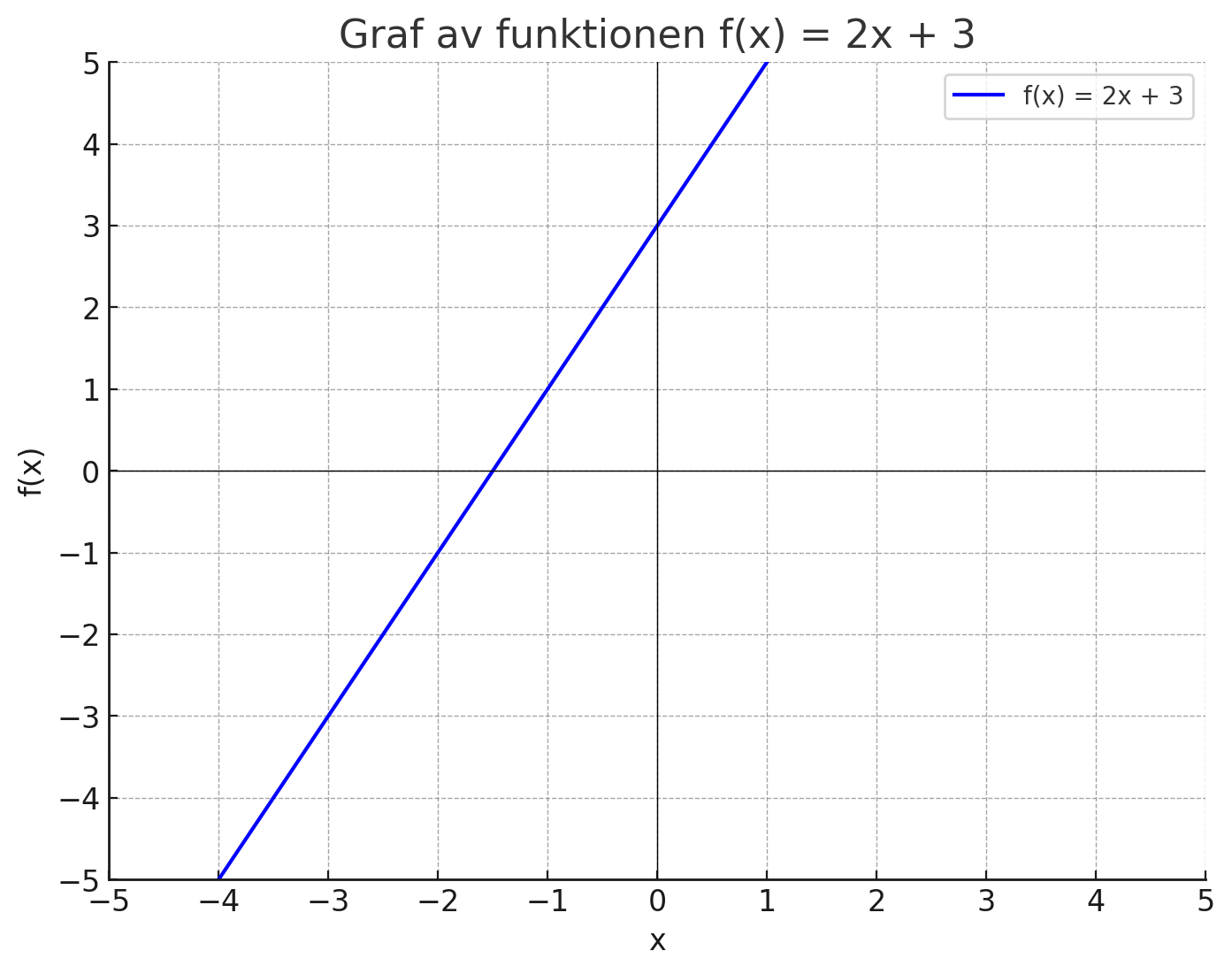
Graf för f(x) = 2x + 3

För att tolka grafen kan vi välja ett x-värde, exempelvis \( x = 1 \). Då kan vi följa den vertikala linjen upp till grafen och se att det motsvarande y-värdet är \( f(1) = 2 \times 1 + 3 = 5 \). Detta visar att när x är 1, är y-värdet 5.

Kvadratisk funktion

En kvadratisk funktion representeras av en parabel och har den allmänna formen:

\[ f(x) = ax^2 + bx + c \]

Grafen för en kvadratisk funktion är en parabel som kan öppna uppåt eller nedåt beroende på tecknet på \( a \). Om \( a > 0 \) öppnar parabeln uppåt, och om \( a < 0 \) öppnar den nedåt. Den kvadratiska funktionen har ett maximum eller minimum beroende på parabelns riktning.

Exempel: \( f(x) = x^2 - 4 \)

Denna funktion har en parabel som öppnar uppåt eftersom koefficienten för \( x^2 \) är positiv. Parabeln skär y-axeln vid \( y = -4 \) och x-axeln vid \( x = -2 \) och \( x = 2 \). Grafen för funktionen ser ut så här:

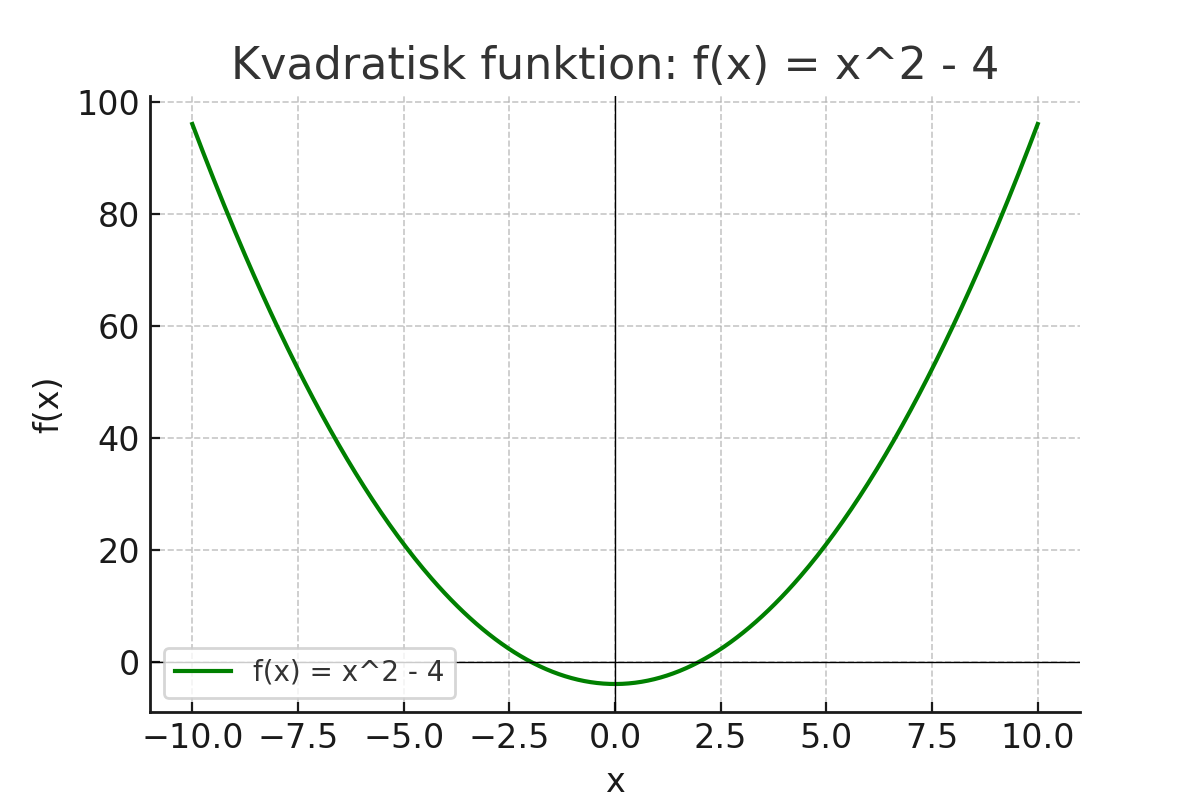
Graf för f(x) = x^2 - 4

För att tolka grafen kan vi välja ett x-värde, exempelvis \( x = 1 \). Då kan vi följa den vertikala linjen upp till grafen och se att det motsvarande y-värdet är \( f(1) = 1^2 - 4 = -3 \). Detta visar att när x är 1, är y-värdet -3. Observera att funktionen är symmetrisk kring y-axeln, vilket innebär att \( f(-1) = f(1) = -3 \).

Exponentialfunktion

Exponentialfunktioner används ofta för att beskriva tillväxt och avtagande. Den allmänna formen för en exponentialfunktion är:

\[ f(x) = a^x \]

Här är basen \( a \) ett positivt tal, och \( x \) är exponenten. Om basen \( a \) är större än 1 växer funktionen exponentiellt, och om basen är mellan 0 och 1 avtar funktionen exponentiellt. Exponentialfunktioner har ofta en brant tillväxt eller avtagande beroende på basens värde.

Exempel: \( f(x) = 2^x \)

Denna funktion växer snabbt eftersom basen är 2. När \( x \) ökar, ökar \( f(x) \) snabbt. Grafen för funktionen ser ut så här:

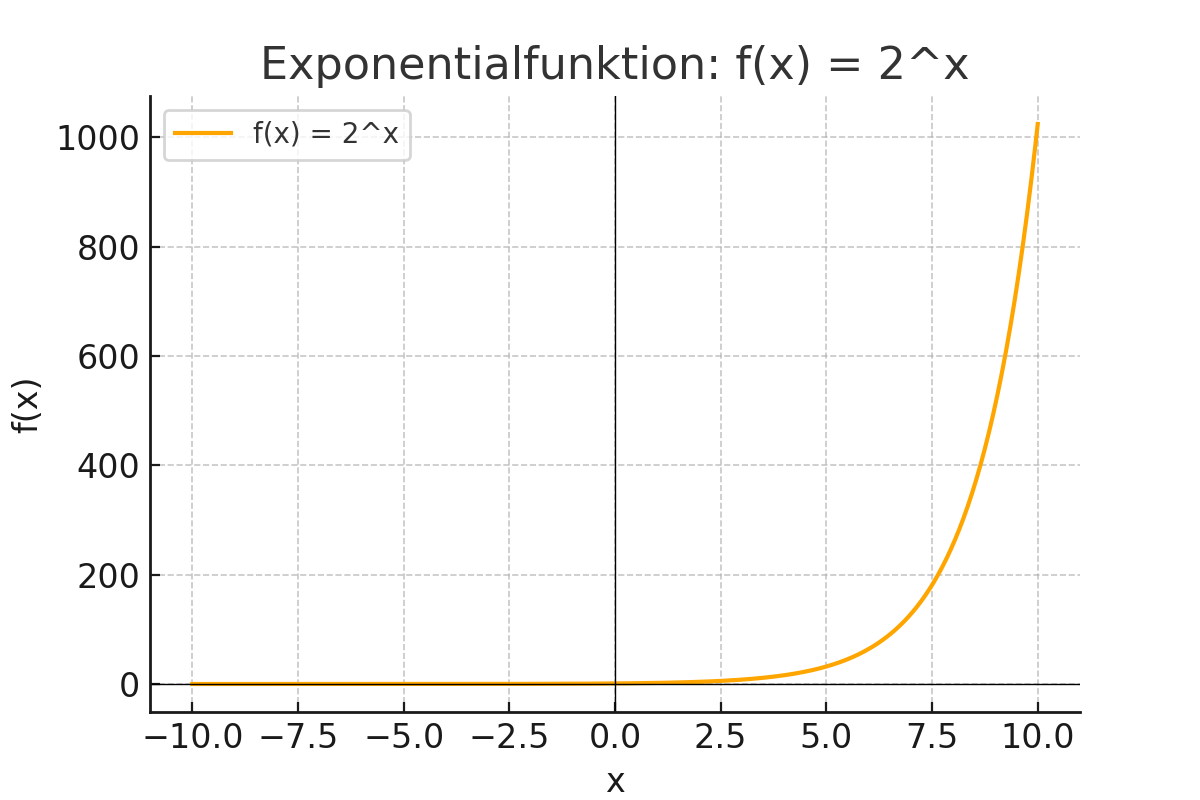
Graf för f(x) = 2^x

För att tolka grafen kan vi välja ett x-värde, exempelvis \( x = 2 \). Då kan vi följa den vertikala linjen upp till grafen och se att det motsvarande y-värdet är \( f(2) = 2^2 = 4 \). Detta visar att när x är 2, är y-värdet 4. Observera hur funktionen växer snabbt när x ökar.

Vanliga frågor

En linjär funktion representeras av en rät linje och beskriver ett konstant samband mellan x och y. En kvadratisk funktion representeras av en parabel och beskriver ett samband där y-värdet förändras kvadratiskt när x-värdet ökar. Linjära funktioner har alltid samma lutning, medan kvadratiska funktioner har en variabel lutning beroende på x.

En exponentialfunktion har en kurva som stiger eller faller snabbt beroende på basen. Om basen är större än 1, stiger grafen brant uppåt. Om basen är mellan 0 och 1, faller grafen snabbt mot x-axeln. Den viktigaste kännetecknet är den exponentiella tillväxten eller minskningen, vilket betyder att y-värdet förändras väldigt snabbt när x ökar.

Nollställen är de punkter där en graf skär x-axeln, alltså där funktionsvärdet (y) är 0. Extrempunkter är antingen maximum eller minimum av en funktion. För en kvadratisk funktion är extrempunkten antingen högsta (maximum) eller lägsta (minimum) punkten på grafen.

Sammanfattning

Att förstå funktioner grafiskt hjälper oss att snabbt analysera deras egenskaper. Genom att känna igen olika typer av funktioner som linjära, kvadratiska och exponentiella, kan vi enkelt förutsäga deras beteende och använda denna information för att lösa olika problem. För varje x-värde kan vi läsa av motsvarande y-värde på grafen, vilket visar funktionens värde vid det specifika x-värdet. Att öva på att tolka grafer kommer att hjälpa dig att bli bekväm med dessa begrepp.