Bestämma räta linjens ekvation från en graf
Snabbguide
- Bestäm lutningen \( k \) genom att ta skillnaden i y och x mellan två punkter: \( k = \frac{\Delta y}{\Delta x} \).
- Hitta skärningspunkten \( m \) med y-axeln genom att leta efter punkten där linjen skär y-axeln, alltså där x är 0.
- Skriv hela ekvationen som \( y = kx + m \) när du har både k och m.
- Kontrollera ekvationen genom att sätta in några punkter från grafen för att se om de uppfyller ekvationen.
Att kunna läsa av en graf och bestämma ekvationen för den linje som representeras är en grundläggande färdighet inom algebra. Räta linjens ekvation har formen:
\[ y = kx + m \]
Här är:
- k: Lutningen på linjen, som beskriver hur mycket y-värdet förändras när x-värdet ökar med 1.
- m: Skärningspunkten med y-axeln, alltså det värde på y när x är 0.
Hur man bestämmer lutningen (k) från en graf
För att bestämma lutningen \( k \) från en graf behöver vi hitta två punkter på linjen. Vi använder dessa punkter för att beräkna förändringen i y-värdet (\( \Delta y \)) och förändringen i x-värdet (\( \Delta x \)). Lutningen beräknas sedan som:
\[ k = \frac{\Delta y}{\Delta x} \]
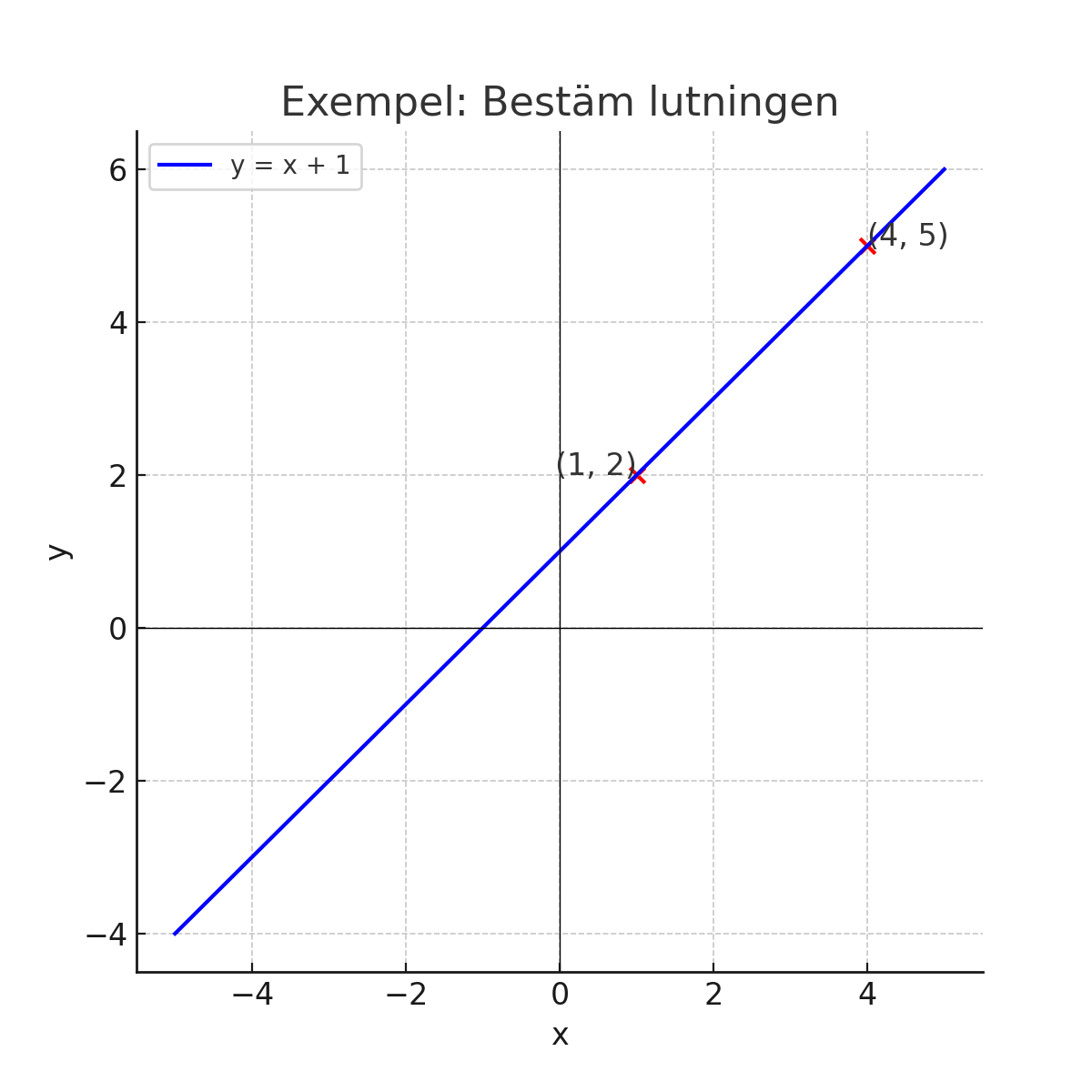
Exempel: Bestämma lutningen från en graf
Anta att vi har en linje som passerar genom punkterna \( (1, 2) \) och \( (4, 5) \). Vi kan beräkna lutningen genom att använda formeln ovan:
\[ \Delta y = 5 - 2 = 3 \]
\[ \Delta x = 4 - 1 = 3 \]
\[ k = \frac{3}{3} = 1 \]
Detta betyder att lutningen på linjen är 1, vilket innebär att y-värdet ökar med 1 för varje enhetsökning i x-värdet.
Hur man bestämmer skärningspunkten med y-axeln (m)
Skärningspunkten med y-axeln, \( m \), är det värde där linjen skär y-axeln. Detta innebär att x-värdet är 0 vid denna punkt. För att hitta m-värdet i grafen, letar vi efter punkten där linjen korsar y-axeln.
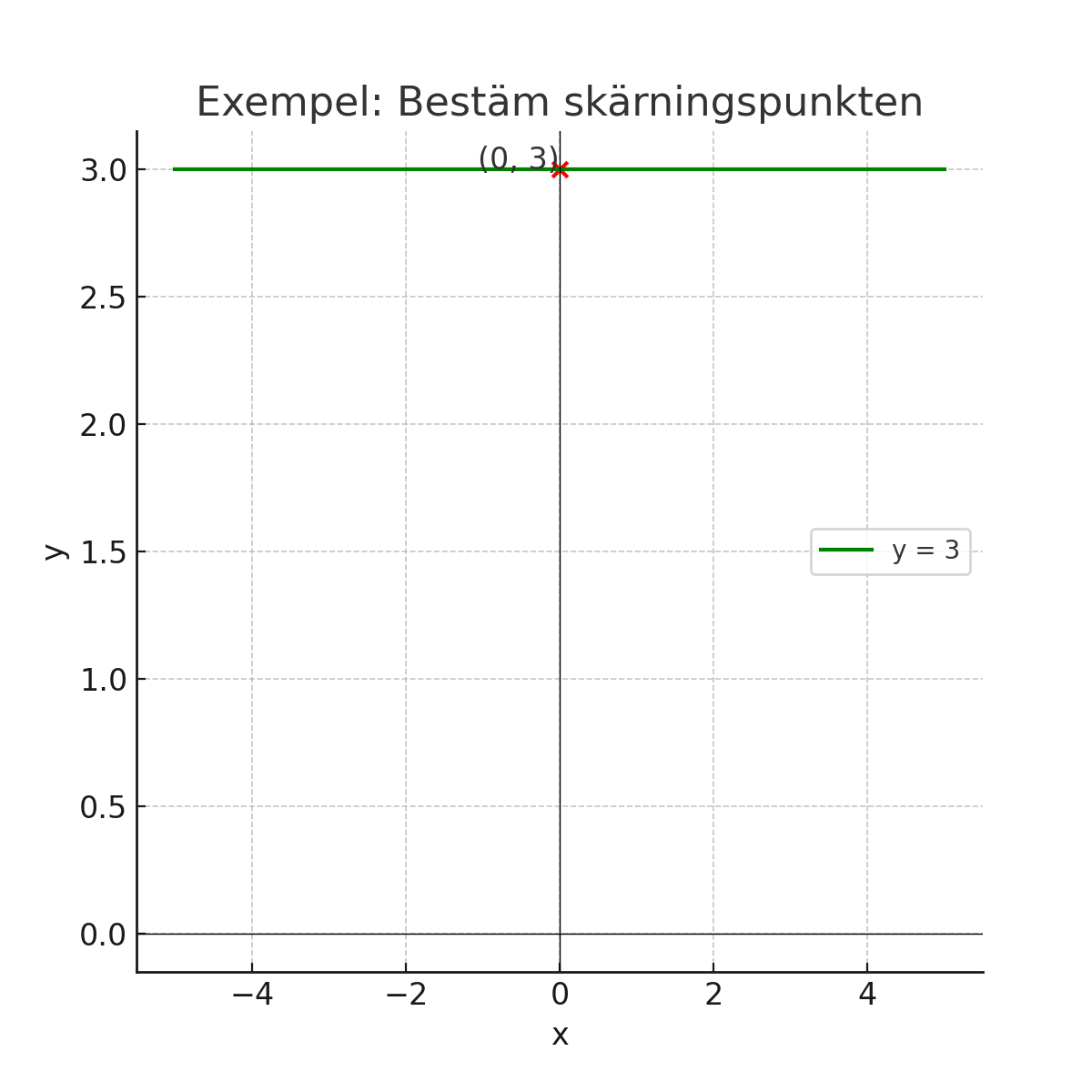
Exempel: Bestämma skärningspunkten med y-axeln
Tänk dig en graf där linjen korsar y-axeln vid punkten \( (0, 3) \). Detta innebär att skärningspunkten är:
\[ m = 3 \]
Detta är m-värdet, vilket är det y-värde där linjen korsar y-axeln.
Bestämma hela ekvationen från en graf
När vi har både lutningen \( k \) och skärningspunkten med y-axeln \( m \) kan vi skriva hela ekvationen för linjen. Låt oss gå igenom ett exempel där vi bestämmer både k och m från en graf och sedan skriver ekvationen.
Exempel: Bestämma ekvationen för en linje
Anta att vi har en linje som går genom punkterna \( (2, 4) \) och \( (4, 8) \) samt skär y-axeln vid \( m = 2 \).
Steg 1: Beräkna lutningen.
\[ k = \frac{8 - 4}{4 - 2} = \frac{4}{2} = 2 \]
Steg 2: Skärningspunkten är redan given som \( m = 2 \).
Steg 3: Sätt samman ekvationen.
\[ y = 2x + 2 \]
Detta är ekvationen för linjen som går genom punkterna och skär y-axeln vid 2.
Vanliga frågor
Sammanfattning
Att bestämma ekvationen för en rät linje från en graf innebär att vi hittar både lutningen \( k \) och skärningspunkten med y-axeln \( m \). Genom att använda två tydliga punkter på linjen kan vi beräkna lutningen som \( \Delta y / \Delta x \), och genom att läsa av var linjen skär y-axeln kan vi hitta m-värdet.