Andragradsfunktioner
Snabbguide
- Andragradsfunktioner har formen \( y = ax^2 + bx + c \) och bildar en parabel.
- Räta linjens ekvation har formen \( y = kx + m \) och är en rak linje.
- En andragradsfunktion öppnar uppåt om \( a > 0 \) och nedåt om \( a < 0 \).
- Vertexen är parabelns toppunkt och kan hittas med \( x = -\frac{b}{2a} \).
- Symmetrilinjen går genom vertexen och delar parabeln i två symmetriska delar.
- För att beräkna ett funktionsvärde, sätt in x-värdet i funktionen.
En andragradsfunktion är en funktion som innehåller en kvadratisk term och har formen:
\[ y = ax^2 + bx + c \]
Där:
- \( a \): Bestämmer parabelns öppning och riktning (uppåt eller nedåt).
- \( b \): Påverkar parabelns lutning och skärningspunkter.
- \( c \): Skärningspunkten med y-axeln, precis som i räta linjens ekvation.
Jämförelse med räta linjens ekvation
Räta linjens ekvation har formen \( y = kx + m \), vilket beskriver en rät linje. I kontrast beskriver en andragradsfunktion en parabel. Här är några viktiga skillnader:
- En rät linje har en konstant lutning (k) och förändras linjärt när x-värdet förändras.
- En parabel har en variabel lutning som beror på x-värdet. Den böjer sig uppåt eller nedåt beroende på tecknet på \( a \).
- En rät linje har en skärningspunkt med y-axeln och kan ha en skärningspunkt med x-axeln. En parabel kan ha 0, 1 eller 2 skärningspunkter med x-axeln beroende på dess form.
Exempel på andragradsfunktion och rät linje
Jämför följande funktioner:
- Räta linjens ekvation: \( y = 2x + 1 \)
- Andragradsfunktion: \( y = x^2 - 2x + 1 \)
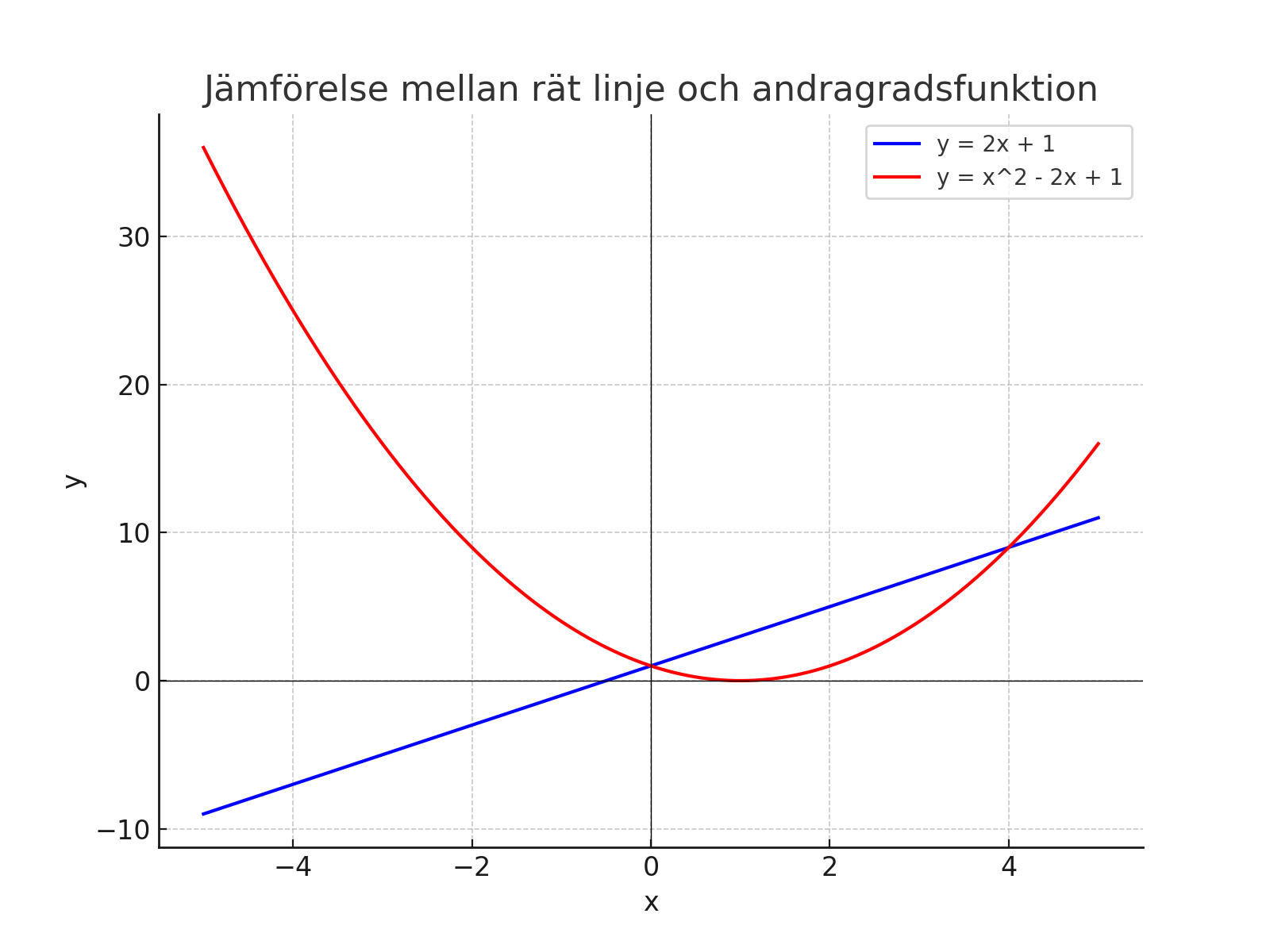
I bilden ovan kan vi se att den räta linjen är en rak linje, medan andragradsfunktionen bildar en parabel.
Grafiska avläsningar av andragradsfunktioner
För att tolka en andragradsfunktion grafiskt kan vi analysera följande egenskaper:
- Vertex (toppunkt): Den högsta eller lägsta punkten på parabeln beroende på om den öppnar uppåt eller nedåt. Vertexen visar var parabeln byter riktning.
- Skärningspunkt med y-axeln: Precis som med räta linjens ekvation är detta c-värdet i funktionen. Det är y-värdet när x = 0.
- Symmetrilinje: En vertikal linje som går genom vertexen. Den delar parabeln i två symmetriska delar.
- Skärningspunkter med x-axeln: Där parabeln korsar x-axeln (där y = 0). Antalet skärningspunkter kan vara 0, 1 eller 2.
Exempel: Grafisk tolkning av andragradsfunktionen \( y = x^2 - 2x + 1 \)
Låt oss analysera funktionen \( y = x^2 - 2x + 1 \):
- Skärningspunkt med y-axeln: När x = 0, är \( y = 1 \). Skärningspunkten är (0, 1).
- Vertex: Funktionen har vertexen (1, 0), vilket är den lägsta punkten på parabeln.
- Symmetrilinje: Symmetrilinjen är x = 1.
- Skärningspunkter med x-axeln: Parabeln korsar x-axeln vid (1, 0).
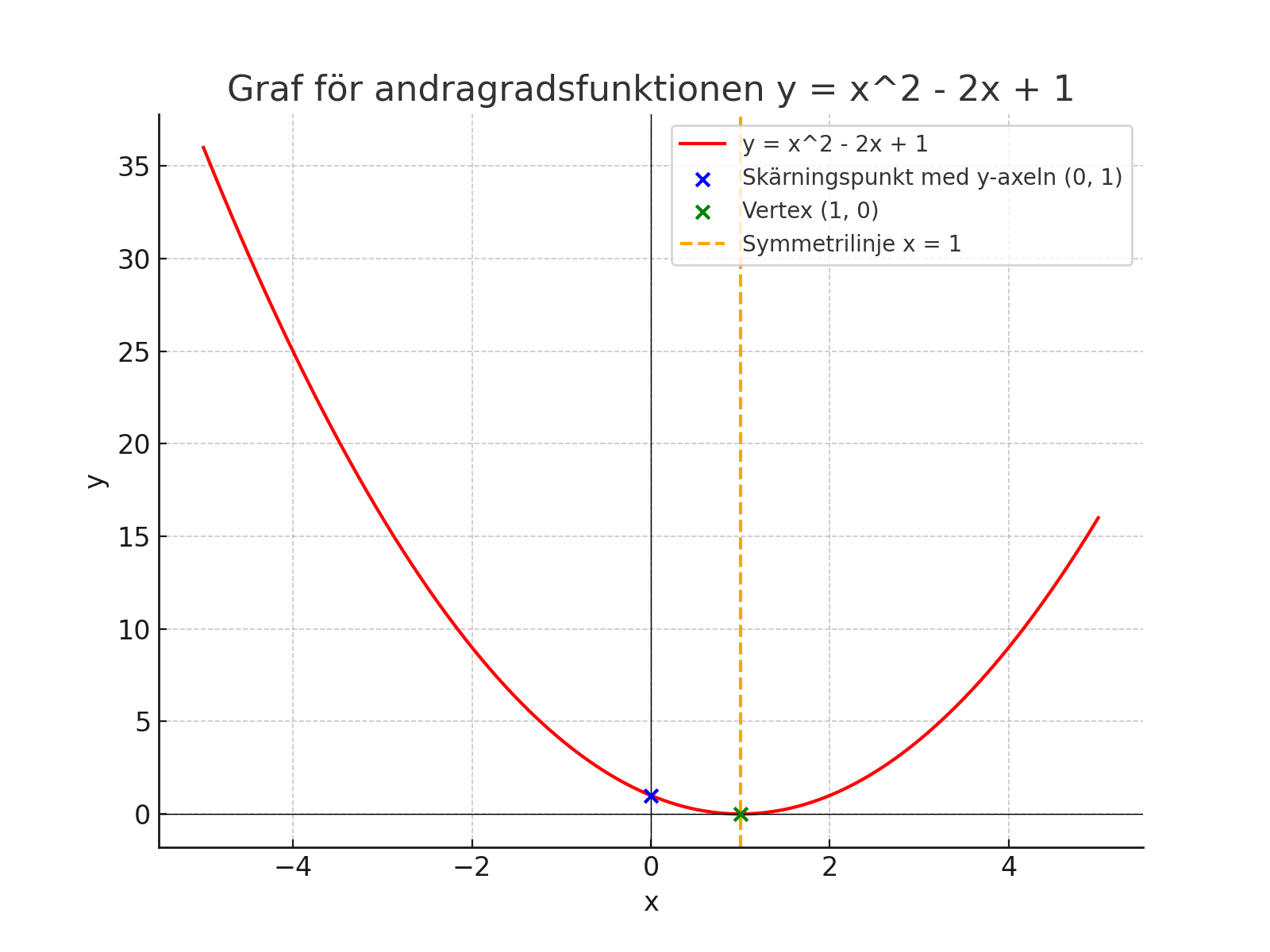
På grafen kan vi se dessa punkter och linjer tydligt markerade.
Sätta in värden i en andragradsfunktion
För att beräkna värdet av en andragradsfunktion för ett givet x-värde, sätter vi helt enkelt in x-värdet i funktionen och räknar ut y-värdet. Låt oss ta några exempel:
Exempel 1: Beräkna \( y = x^2 - 2x + 1 \) när \( x = 2 \)
Lösning:
\[ y = 2^2 - 2 \times 2 + 1 = 4 - 4 + 1 = 1 \]
När \( x = 2 \), är \( y = 1 \).
Exempel 2: Beräkna \( y = x^2 - 2x + 1 \) när \( x = -1 \)
Lösning:
\[ y = (-1)^2 - 2 \times (-1) + 1 = 1 + 2 + 1 = 4 \]
När \( x = -1 \), är \( y = 4 \).
Vanliga frågor
- Om \( D > 0 \) finns två skärningspunkter.
- Om \( D = 0 \) finns en skärningspunkt (dubbla rötter).
- Om \( D < 0 \) finns inga skärningspunkter.
Sammanfattning
Andragradsfunktioner skiljer sig från räta linjens ekvation genom att de beskriver en parabel istället för en rak linje. Genom att förstå deras grafiska representation kan vi analysera deras egenskaper och skärningspunkter.