Ekvationssystem och grafisk lösning
Ett ekvationssystem består av två eller flera ekvationer som är sammanlänkade med varandra. Målet är att hitta ett gemensamt värde för variablerna som uppfyller alla ekvationer i systemet. Ett sätt att lösa ekvationssystem är genom att använda en grafisk metod, där vi hittar skärningspunkten mellan graferna för ekvationerna. Denna metod är nog den som går fortast vilket kan vara till stor fördel på HP (högskoleprovet) med tanke på tidspressen som provet bär med sig.
Snabbguide
- Ekvationssystem: Två eller flera ekvationer som är sammanlänkade.
- Grafisk lösning: Rita graferna och hitta skärningspunkten.
- Skärningspunkt: Lösningen på ekvationssystemet, där båda ekvationerna är sanna samtidigt.
Vad är ett ekvationssystem?
Ett ekvationssystem kan beskrivas med två eller flera ekvationer, till exempel:
\[ \begin{cases} y = 2x + 1 \\ y = -x + 4 \end{cases} \]
Målet är att hitta den punkt \((x, y)\) där båda ekvationerna är sanna samtidigt. Detta kan vi göra genom att rita graferna för båda ekvationerna i ett koordinatsystem och leta efter skärningspunkten.
Grafisk lösning av ekvationssystem
För att lösa ett ekvationssystem grafiskt ritar vi upp graferna för de båda ekvationerna i ett koordinatsystem. Där graferna skär varandra finns den gemensamma lösningen.
Exempel: Lösning av ekvationssystem grafiskt
Vi har ekvationssystemet:
\[ \begin{cases} y = 2x + 1 \\ y = -x + 4 \end{cases} \]
Rita graferna för båda ekvationerna i samma koordinatsystem. Precis som nedan:
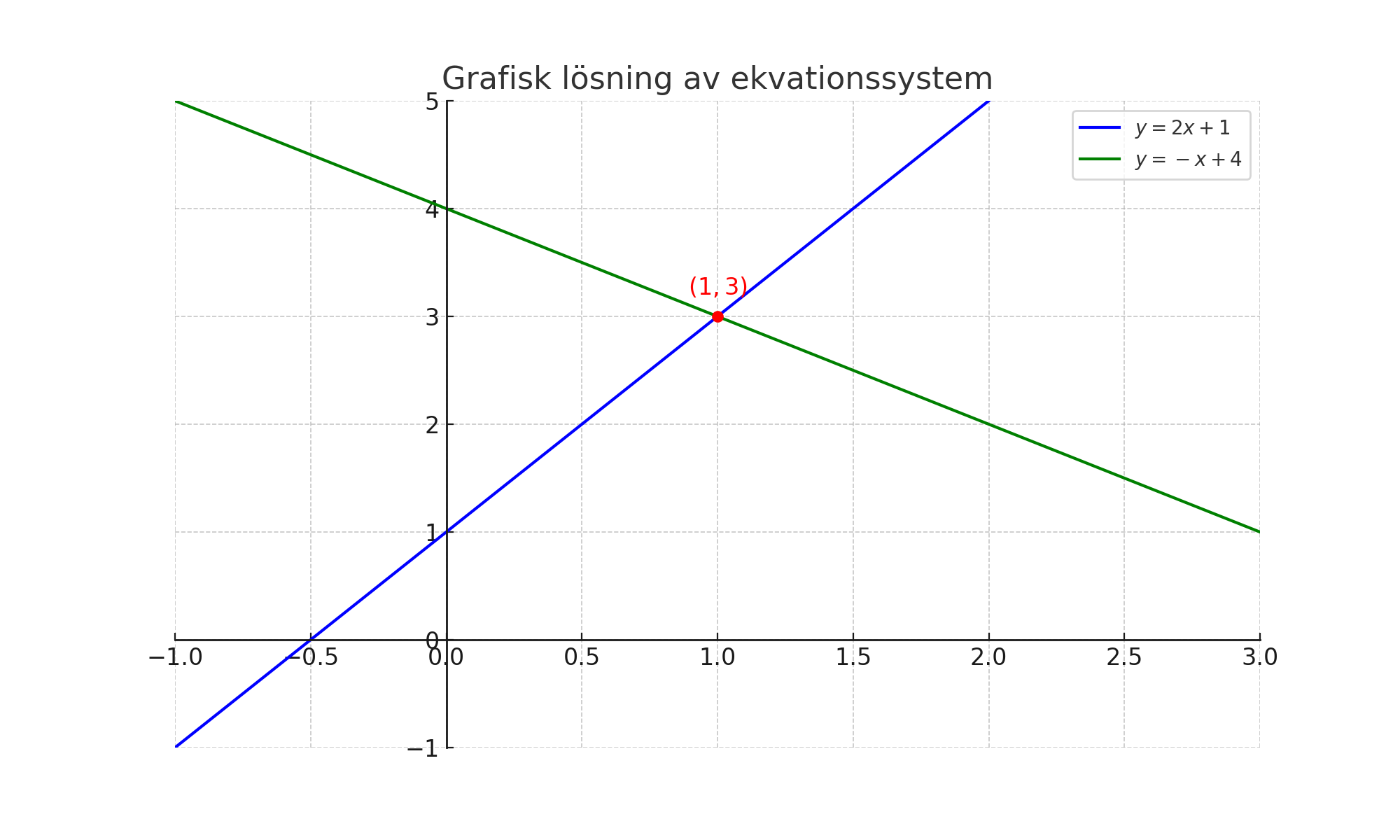
Vi ser att linjerna skär varandra i punkten \( (1, 3) \). Det betyder att lösningen på ekvationssystemet är \( x = 1 \) och \( y = 3 \).
Hur ritar man grafer för ekvationerna?
Läs allt om räta linjens ekvation och funktioner samt grafiska lösningar under kursen om funktioner.
För att rita graferna för ekvationerna behöver vi välja några punkter som uppfyller varje ekvation. Till exempel, för ekvationen \( y = 2x + 1 \) kan vi välja följande punkter:
- Om \( x = 0 \), då är \( y = 2 \cdot 0 + 1 = 1 \). Punkterna är \( (0, 1) \).
- Om \( x = 1 \), då är \( y = 2 \cdot 1 + 1 = 3 \). Punkterna är \( (1, 3) \).
- Om \( x = -1 \), då är \( y = 2 \cdot (-1) + 1 = -1 \). Punkterna är \( (-1, -1) \).
För ekvationen \( y = -x + 4 \) kan vi välja följande punkter:
- Om \( x = 0 \), då är \( y = -0 + 4 = 4 \). Punkterna är \( (0, 4) \).
- Om \( x = 1 \), då är \( y = -1 + 4 = 3 \). Punkterna är \( (1, 3) \).
- Om \( x = 2 \), då är \( y = -2 + 4 = 2 \). Punkterna är \( (2, 2) \).
Rita linjerna i ett koordinatsystem
För att rita linjerna i ett koordinatsystem markerar vi punkterna och drar en linje genom dem. På så sätt kan vi se var linjerna skär varandra som i bilden nedan:
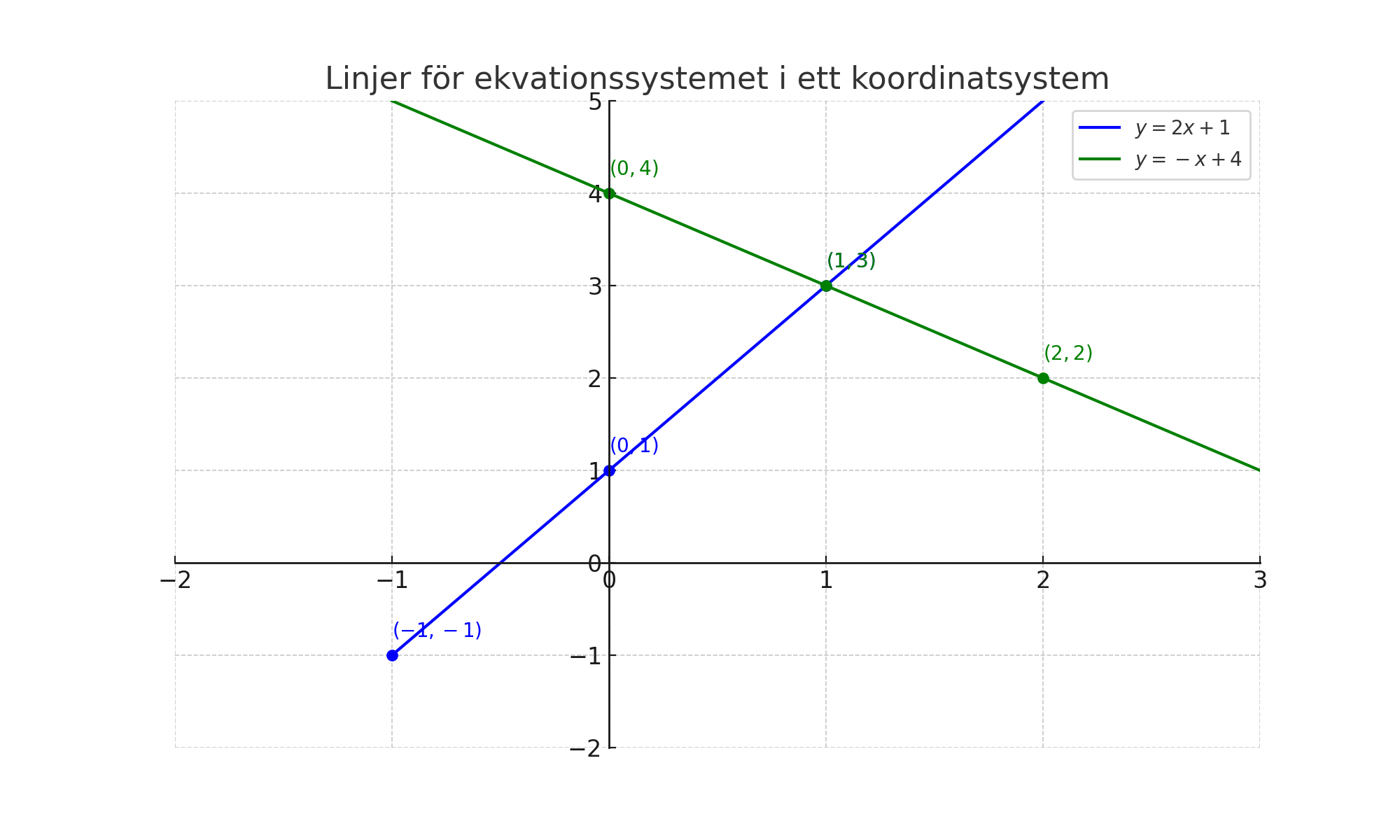
Vanliga frågor
Sammanfattning
Grafisk lösning av ekvationssystem är ett visuellt sätt att hitta en gemensam lösning för två eller flera ekvationer. Genom att rita graferna och hitta skärningspunkten kan vi se var ekvationerna har samma värden.